ยินดีต้อนรับทุกท่าน เข้าสู่ เว็บแทงหวยออนไลน์ชั้นนำอันดับ 1 ของไทยที่จ่ายแพงที่สุด 2022
แทงหวยออนไลน์ กับ 999LUCKY เว็บแทงหวยออนไลน์ที่ดีที่สุด ของไทย เราเปิดให้บริการ แทงหวยออนไลน์ มานานมากกว่า 10ปี จึงได้เป็นที่นิยมของนักเล่นหวยน้อยใหญ่ไม่ว่าใครก็สนใจเข้ามาใช้บริการเล่นหวยออนไลน์เรามีหวยออนไลน์ครบวงจรเปิดให้บริการอีกด้วยไม่ว่าจะเป็น หวยลาว หวยรัฐบาลไทย หวยเวียดนาม หวยปิงปอง หวยมาเลย์ หวยหวยหุ้นไทย หวยหุ้นดาวโจนส์ หวยหุ้นต่างประเทศ และ หวยลัคกี้เฮง หวยน้องใหม่มาแรง2022 เปิดให้บริการเล่นกันแบบไม่มีเบื่อ
เว็บหวยชั้นนำ 999LUCKY จ่ายจริง จ่ายหนัก การเงินมั่นคง เชื่อถือได้ ปลอดภัยแน่นอนแทงหวยออนไลน์ กับ 999LUCKYได้ง่ายมากไม่ยุ่งยากอย่างที่คิด เรามีระบบฝาก-ถอนเงิน อัตโนมัติรวดเร็วด้วยโปรแกรม ที่นำเข้าจากประเทศอังกษฤ บอกเลยว่าอัพเดทเว็บไซต์รวดเร็วที่สุด ไม่ว่าท่านจะอยู่ที่ไหนก็สามารถเล่นหวยออนไลน์ได้ผ่านระบบสมาร์ทโฟนมือถือได้ทุกยีห้อ
เราจะคอยย้ำพนักงาน เรื่องการดูแลใส่ใจลูกค้าก่อนเสมอ จึงได้เป็นที่สนใจของบรรดานักเล่นหวยทั่วสาระทิศต่างนิยมเข้ามาแทงหวยออนไลน์ กับ 999LUCKY ชื่อนี้จำให้ดีเราเท่านั้นที่กล้าให้
แทงหวยออนไลน์ ราคาสูงส่วนลดเยอะต้อง แทงหวยออนไลน์ 999LUCKY เท่านั้น !
- ระบบฝาก-ถอนอัตโนมัติทันสมัยรวดเร็วทันใจ
- รับแทงหวยออนไลน์ อย่างเต็มรูปแบบ
- แทงเป็นล้านถูกเป็นล้าน เราพร้อมจ่ายในทันที
- การเงินมั่นคง จ่ายจริง ไม่โกง ปลอดภัย100%
- มีหวยยี่กี ออกผลด้วยตัวเองได้
- ใช้ Cloud Server อย่างเต็มรูปแบบ
- ระบบสำรองข้อมูลลูกค้า Ail Time เงินไม่หายปลอดภัยแน่นอน
- แจกโบนัสโปรโมชั่นสุดพิเศษอีกมากมาย
- ฝาก 1บาทก็สามารถแทงหวยกับเราได้
- เรามีทีมงานประสบการณ์สูงชำนานเรื่องหวยออนไลน์ โดยตรงมากกว่า 8ปี
แทงหวยออนไลน์ กับ 999LUCKY บอกว่าเลยท่านไม่มีหผิดหวังแน่นอน เรามีพนักมากมายที่รองรับลูกค้านับหมื่นคน ไม่ต้องห่วงเราจะเน้นย้ำพนักงานของเรานั้นตลอด เรื่องการบริกการดูแลใส่ใจลูกค้าที่เข้าใช้บริการแทงหวยออนไลน์กันเป็นหลักเสมอถ้าเกิดปัญหา หรือสงสัยอะไรเกี่ยวกับเว็บแทงหวยออนไลน์เรา ท่านสามารถแจ้งพนักงาน หรือ ติดต่อเรา ที่หน้าหลักของเว็บไซต์แค่กดที่เมนู ติดต่อสอบถาม เรามีทีมการให้คำปรึกษาตลอด 24 ช.ม สมัครสมาชิก ฟรี !
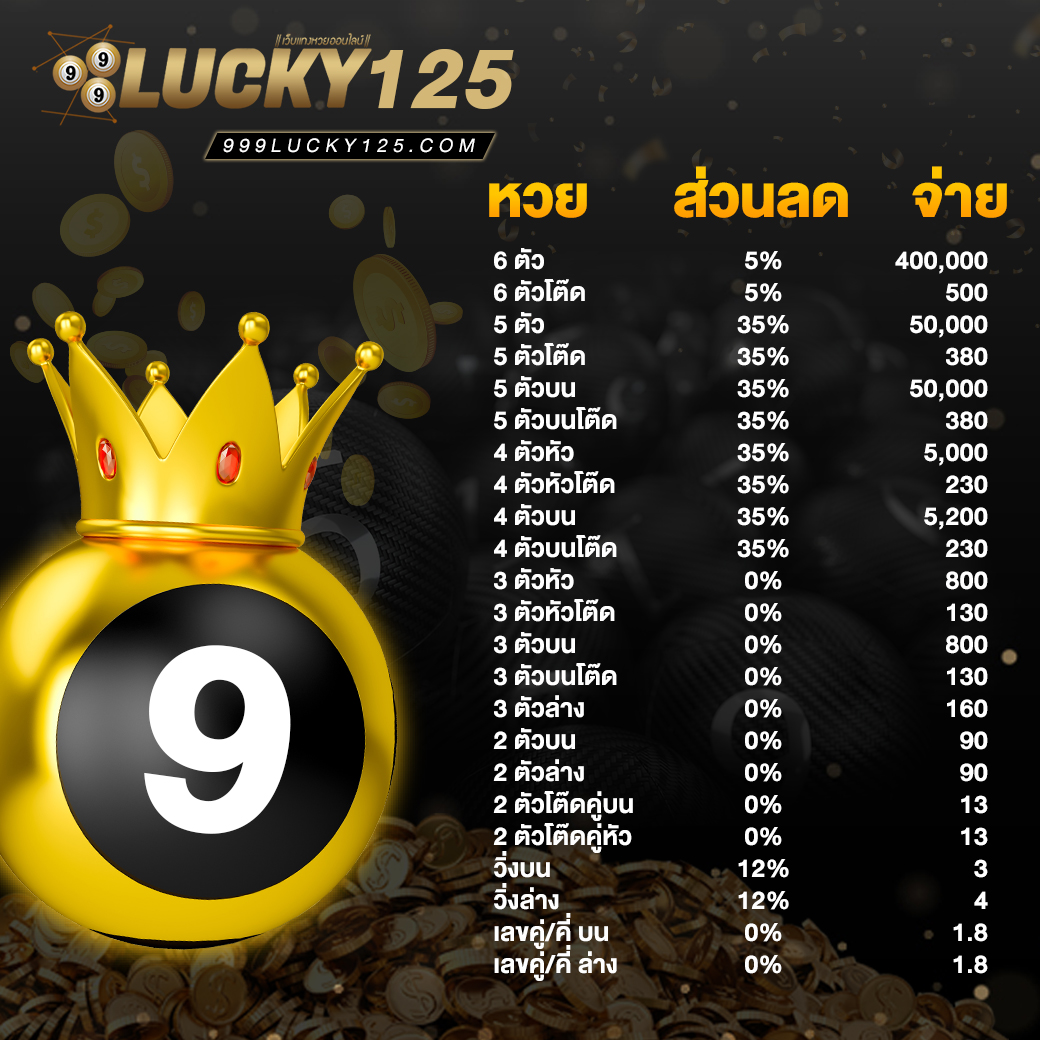
ราคาหวยดีที่สุด ราคาจ่ายเยอะ เล่นหวยออนไลน์ กับ 999LUCKY เท่านั้น
หวยรัฐบาลไทย หวยลัคกี้เฮง หวยปิงปอง หวยหุ้นดาวโจนส์
โปรโมชั่นใหม่ AFFมีเพื่อนแนะนำมาสมัครสมาชิก รับโบนัสสูงสุด 5%
อัพเดทผลหวยเร็ว ระบบเว็บไซต์แทงหวยออนไลน์ ที่กำลังครองใจคนทั้งประเทศ